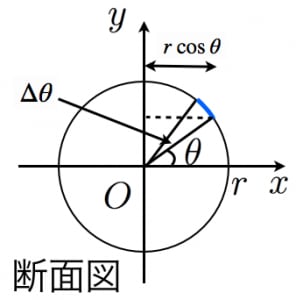
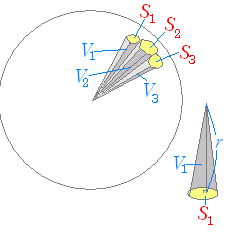
球の表面積 = 円周 × 極間の距離 × 2 π ってことをやった。 どちらも 底辺 × 高さ × 定数 の形だね。 これを用いて、「球の表面積=円の面積×4」の説明をしてみよう。 まず、考えやすいように次のような プラネタリウム 型の図形を考えてみよう。 いま示せばいいのは、「半球の表面積=円の面積×2」です。 さっきも書いたように、円周を底辺としたときなので球の面積は となります。よって、球と円柱の面積が同じなので、球の表面積は となります。 球の体積の証明 続いて、球の体積の公式の証明を行います。半径 の球を図のように正四角錐に分けていきます。 するとひとつの錐体の体積は となります。S:球の体積からスイカの様に三角錐を作って表面積を求めるしかないのかな。 t:球面三角法で球面の三角形の面積を求める公式を使えばできるかも。 s:でも、最初の三角形の面積の公式が求まるよ。 2 だから、α=2/π =底辺×r

もっちゃんと数学 球の体積はなぜ 4pr 3 3なの 中学範囲で Youtube
球の体積 表面積 公式 なぜ
球の体積 表面積 公式 なぜ-球の体積の公式から、表面積Sは、 (4/3) π r 3 = (1/3)・S・r より、S = 4 π r 2 以上から、 (球の表面積) = 4 π r 2 という公式が作られる。 球の体積、表面積については、いろいろな覚え方があるが、次は、有名でしょう。円周の長さと円の面積は、小学校6年生で登場するが、球の計量は扱わない。球の表面積・体積が登場する のは、中学校1年生の 数学からである。いずれもその計量の公式 表面積 S=4πr^2 , 体積




微分でつなげる円や球の公式 すうがくブログ 式変形ch
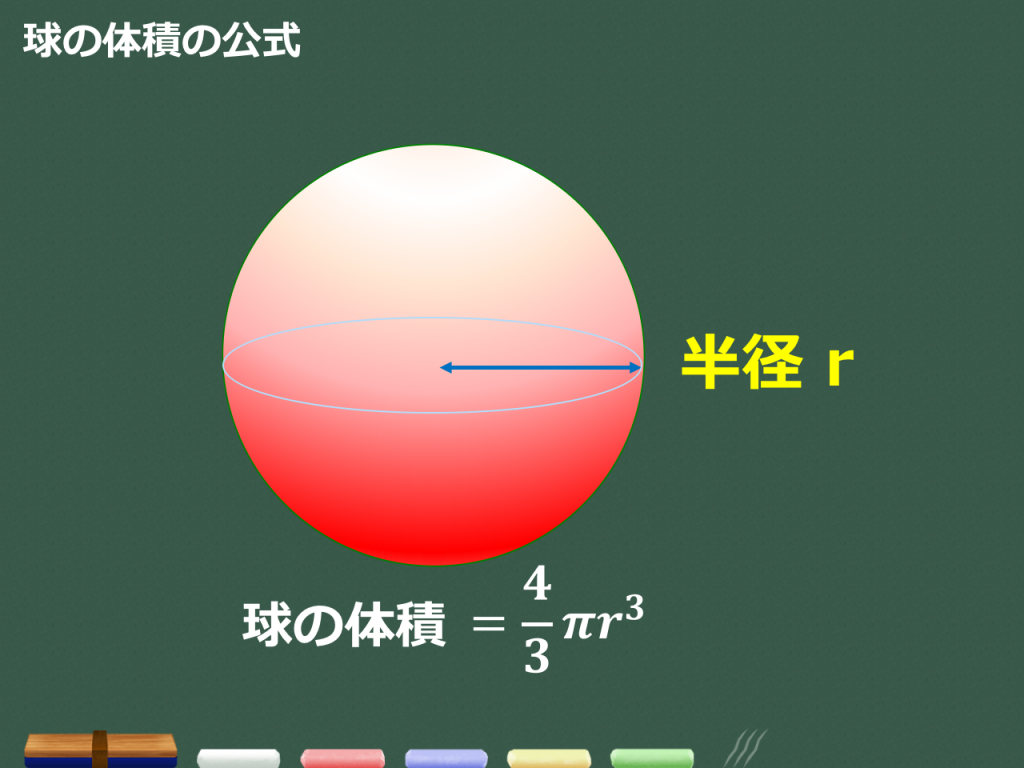
という語呂で「球の体積の公式(3分の4 × 円周率 × 半径の三乗)」をおぼえてしまおう。 テスト前にがんばって暗記してみてね^^ そんじゃねー Ken なぜ球の公式がつかえるのか気になったらみてみて↓球の体積と表面積 半径 \\(r\\) の球の体積と表面積を求める公式は以下のようになります。 \\(球の体積=\\displaystyle \\frac43\\pi r^3\\) \\(球の表面積=4\\pi r^2\\) 「なぜこの公式が成立するのか」については中学生の知識の範囲外です。 球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4 π r 2 4\pi r^2 4 π r 2 →「心配アール二乗」 球の体積: 4 3 π r 3 \dfrac{4}{3}\pi r^3 3 4 π r 3 →「身の上に心配アール三乗」
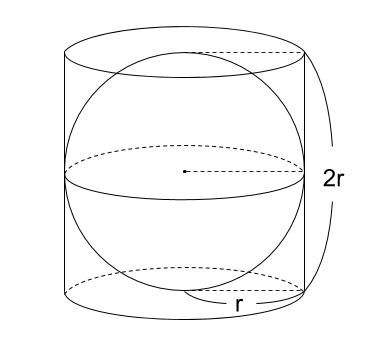
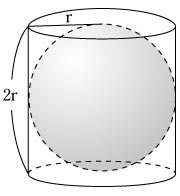
表面積 表面積を求める方法として,次の方法がよく知られている。 半径r の球にひもを巻き付けて,それを平面上で巻き直すと,半径が2r の渦巻きになる。ひも の占める面積は球の表面積に等しいから,球の表面積はπ(2r)2 = 4πr2 である。円柱・円錐・半球の断面積の,不思議な関係とは? 球の体積は,どうやって求められる? 球の表面積は,どうやって求められる? coffee break 錐体の体積の公式は,なぜ「1/3」をかける? こんにちは。相城です。今回は球の表面積について書いていこうと思います。 中学生でも納得かな?なぜ球の表面積は なのかを証明しよう。 先ず半径, 中心角 の扇形から, 半径, 中心角 の扇形を引いた面積 は次の式で表される。 ただし は幅 の部分の中央線である。球の表面積の公式と語
Yo 1047 280 この動画を見れば分かります。 「 球の表面積が円の面積の4倍であることの証明 」 すごいwww なるほど、すごいですね。 そのような証明方法があったとはw 謎がやっと解決しました。 やはり、言葉より図のほう球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半 高校数学 kanrinin 微分でつなげる円や球の公式 今回の内容の動画版です→球の体積公式の微分が表面積になっている理由 円の面積、円周の長さおよび球の体積、表面積は次のように計算できます。




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




微分でつなげる円や球の公式 すうがくブログ 式変形ch
」 とある。平成15年実施の学習指導要領から、「 球の体積」 は高校の数学Ⅰへと移行になった。「 高等学校学習指導要領解説 数学編 理数編」には、 「球の表面積と体積については、単に公式を示し、それを利用するという技術的な扱いだ球の体積公式の微分が表面積になっている理由 球の体積公式の微分が表面積になっている理由 Watch later Share Copy link Info Shopping Tap to半径 r の球の表面積は、次の式で求められます。 球の表面積 \begin{align*} S = 4\pi r^2 \end{align*} 表面積 = 4 × 314 × 半径 × 半径 公式の導出方法と計算例については、「球の表面積の求め方」をご覧




もっちゃんと数学 球の体積はなぜ 4pr 3 3なの 中学範囲で Youtube



1
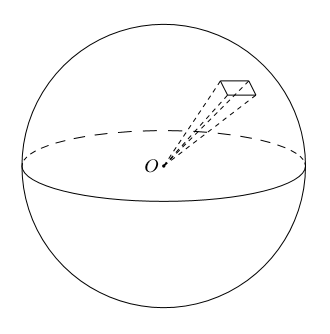
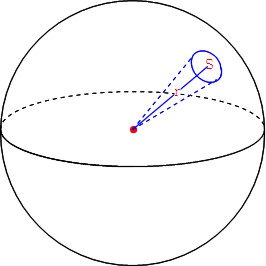
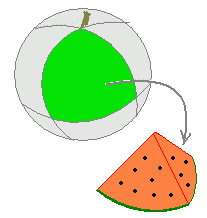
7、球の表面積 T:ところで、球の体積がわかると、球の表面積もわかる。 s:球は曲がっているのに、表面積が求まるんですか。 T:夏になるとスイカを食べるだろ。あのスイカを食べやすくするために切るね。そのスイカ をどんどん小さくしていく。する 球の体積の公式のなぜ? 球の中心を とし、頂点を とする正四角錐で球を 等分していくことを考える。 このとき、 を無限に近づけていくと、四角錐の高さは球の半径 に限りなく等しくなる。また、球の表面積は 等分される。 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jinOther than the above, but not suitable for the Qiita community (violation of guidelines)球欠 (spherical




球の表面積と体積の公式 数学fun




球の表面積の公式について みたにっき はてな
下図のように切り込みを入れてはがす。 横の長さ=球の一周分の長さ= 2πr 縦の長さ=球の半周分の長さ= πr 形を単純にしてだいたいの面積を求める. 面積= πr × 2πr × 1 2 = π2r2 = 314πr2 形を切り落として考えているため,実際の面積はもう少し大きいと考えられる. 球体の表面積 S > 314πr2 (1) 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するため半径r の円の面積 r2 をr で微分すると, 2 r となり,円周の長さ公式になる。同様に半径 r の 体積の公式 3 3 4 r をr で微分すると 4 r2 となり,球の表面積の公式となる。 しかし,一辺の長さ xの立方体の体積 x3 をxで微分しても表面積 6x2 にはならない。その



1



球の表面積 球の表面積 4pr 2という公式がありますが なぜそうなるので Yahoo 知恵袋
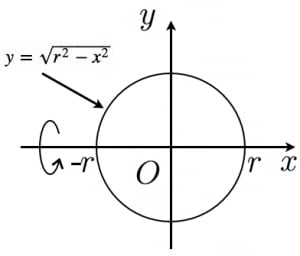
球の体積の求め方でなぜ3分の4が出てくるのかわかりません。 中1でもわかるように説明お願いします (>人<;) 縮め る球の表面積と体積 解く前に確認しよう ④ 球の表面積 半径が7の球の表面積をねとすると ぐー477" ④ 球の体積 半径が7の球の体積をしと①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r球の体積と表面積にについて 1 はじめに 皆さん!どうして半径rの球の体積や表面積が( πr 3 や4πr 2 になるのか不思議に思ったことはありませんか。ここで、一体誰がこのような結果にたどり着くような考え方をしたのかを、今から本を読んで知り得たこと




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



球の体積と表面積を積分で証明 高校数学の美しい物語
球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積) \(\displaystyle \frac {6}{D \rho}\) 半分以上隠れている円の直径の推定 接触角の概算 円と球の空間




球の体積と表面積1 3教材keynote Youtube




角錐 円錐の体積と表面積の公式 数学fun




球に関する公式 理数系無料オンライン学習 Kori




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく




球の体積の求め方でなぜ3分の4が出てくるのかわかりません 中1でもわかるように説明お Clear




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



Mathematics 球の体積と表面積を求める公式 働きアリ




Mathematics 球の体積と表面積を求める公式 働きアリ



中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




球の体積の公式を積分を使わず導く 中受でも出るかも 兄中学生活




初等幾何 球の表面積を求める 大人が学び直す数学




173 1 なぜ微分するんですか 教えてください Clear



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




球の体積 球の表面積の公式の導出 積分 優技録




球体の体積 中学生に分かるように真剣に考えてみた うちーノート



球の体積が4 3 表面積が4なのはなぜか教えてください ただし Yahoo 知恵袋




数学講師必見 中学数学でも必須 球の体積 表面積の覚え方と導出まとめ 高校数学 塾講師ステーション情報局




球の表面積と体積の公式 数学fun




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ



中学数学 球の体積の何で 数樂管理人のブログ




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館




球体の表面積 中学生に分かるように真剣に考えてみた うちーノート




球の体積 球の表面積の公式の導出 積分 優技録




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
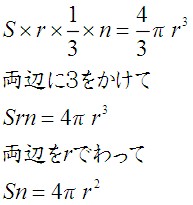



Mathematics 球の体積と表面積を求める公式 働きアリ




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



数学 球の表面積を積分で計算してもうまくいかない人へ




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




球の体積と表面積 公式と計算問題と証明 Irohabook




球の体積 表面積 無料で使える中学学習プリント




球の表面積と体積の公式 数学fun




半球の体積と表面積を計算する 具体例で学ぶ数学




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球体の表面積 中学生に分かるように真剣に考えてみた うちーノート




球の体積と表面積 Youtube



例題対比 球の体積と表面積



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



研究



研究




球の体積と表面積を積分で証明 高校数学の美しい物語




球の体積 表面積 中1数学 空間図形9 Youtube



球の表面積の公式 中2男子です なぜ球の表面積の公式は4 Yahoo 知恵袋




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積を微分すると表面積に 円の面積を微分する円周になるのはなぜか いぬおさんのおもしろ数学実験室



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ



Mathematics 球の体積と表面積を求める公式 働きアリ



球の表面積の公式の求め方




球の表面積の公式について みたにっき はてな



数学トピックq A




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の表面積と体積の公式 数学fun




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ



球の体積と表面積を積分で証明 高校数学の美しい物語




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



例題対比 球の体積と表面積




中学数学 球の体積の何で 数樂管理人のブログ




球の体積と表面積 Jsciencer




球の体積と表面積 公式と計算問題と証明 Irohabook




Excel エクセルで球の体積と表面積を計算する方法 モッカイ




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




球の表面積の求め方 公式と計算例



1



数学 球の表面積を積分で計算してもうまくいかない人へ




中1 中一数学 球の表面積と体積 中学生 数学のノート Clear




球の表面積と体積の公式 数学fun




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




中1 数学 6 5 球の体積 表面積 Youtube



1




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




球の体積と表面積 Jsciencer




Hd限定円錐 体積 求め方 裏ワザ 最高のぬりえ




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




角錐 円錐の体積と表面積の公式 数学fun




面白数学 球の表面積 円の面積 4の理由 東大生の高校数学ブログ




球の体積を微分すると表面積に 円の面積を微分する円周になるのはなぜか いぬおさんのおもしろ数学実験室




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく
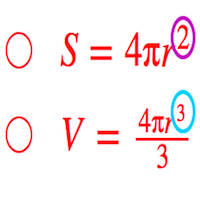



球の表面積と体積の求め方 苦手な数学を簡単に
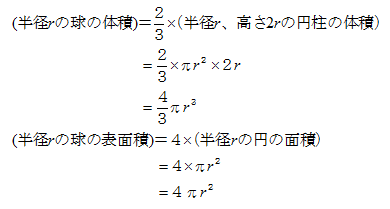



授業実践記録 数学 球の体積 表面積 実験から公式を 啓林館




100 Epic Best円錐 の 体積 公式 最高のぬりえ



球の表面積の公式の求め方




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



0 件のコメント:
コメントを投稿