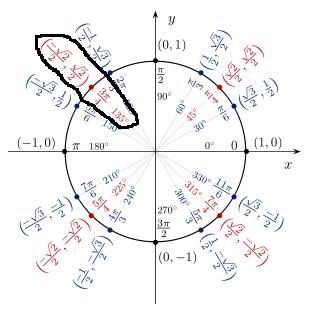
Suppose that both f 00 and g 00 are continuous for all xvalues on −1, √ 3 2 Suppose that the only local extrema that f has on the interval −1, √ 3 2 is a local minimum at x = 1 2 (a) (4 pts) Determine the open intervals of increasing and decreasing for g on the interval h 1 2 , √ 3 2 iThe angles of a quadrilateral are in the ratio 3 5 9 1;Sin 30°= 1/2 cos 30° = √3/2 tan 30° = √3/3 csc 30° = 2 sec 30° = 2√3/3 cot 30° = √3 30/60/90 triangle ratios in terms of degrees from the 60°
Solve Equations With Square Roots Elementary Algebra
2/3 - 1/2 as a fraction
2/3 - 1/2 as a fraction- 1/2 equals 05, meaning B's also not it We also know the answer isn't D, since 0 does not equal 1 That only leaves C Yet when check, just in case, √3/2 equals , meaning that's not the answer We've eliminated every answer so far, meaning we should go back and check our workQuestion If the terminal side of an angle θ in standard position intersects the trigonometric circumference at the point P (−1 / 2, √3 /
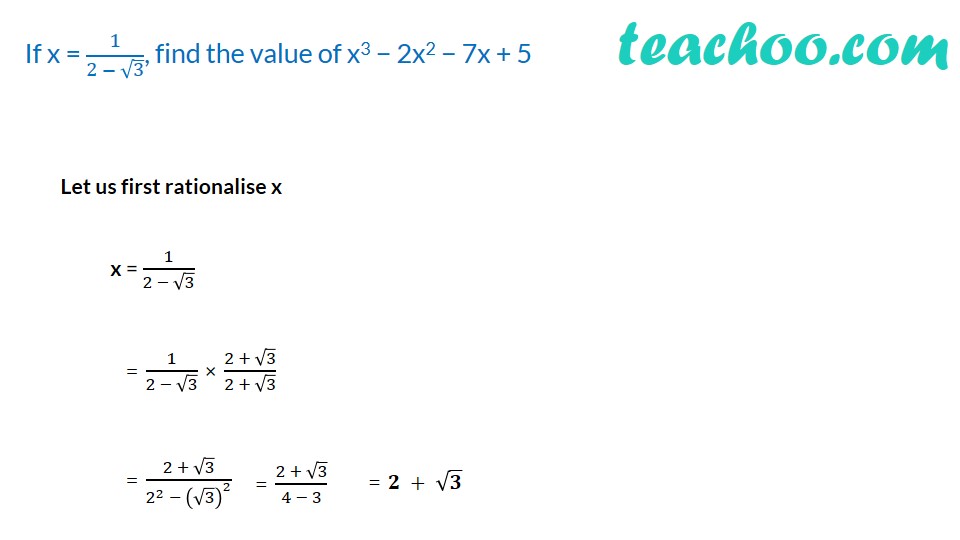



If X 1 2 3 Find The Value Of X 3 2x 2 7x 5 Video T
Haz clic aquí 👆 para obtener una respuesta a tu pregunta ️ Si tan(4x) cot(x 60°) = 1, calcular "sen3x" a) 1/2 b) √3/2 c) 3/5 d) √2/2 e) NASine calculator online sin(x) calculator This website uses cookies to improve your experience, analyze traffic and display ads(22𝑖) 𝑖 (60°)=(22𝑖)(1 2 𝑖√3 2) (22𝑖) 𝑖 (60°)=1𝑖√3𝑖−√3 (22𝑖) 𝑖 (60°)=(1−√3)𝑖(1√3) √Translating the point 2 units left and 𝑖 unit down → (1− 3)𝑖(1√3) Hence the answer is C 14 The determinant of a triangular matrix is the product along the main diagonal
Next consider 30° and 60° angles In a 30°60°90° right triangle, the ratios of the sides are 1 √3 2 It follows that sin 30° = cos 60° = 1/2, and sin 60° = cos 30° = √3 / 2 These findings are recorded in this table If i = √(1) then 4 5(1/2 i√3/2) 334 3(1/2 i√3/2) 365 is equals to (a) 1 – i√3 (b) 1 i√3 (c) i√3 (d) i√3 Answer Answer (c) i√3 Given, 4 5(1/2 i√3/2) 334 3(1/2 i√3/2) 365 = 4 5w 334 3w 365 {since w = 1/2 i√3/2} = 4 5w 3w² {since w³ = 1}Determine angle type 74 is an acute angle since it is less than 90° sin (74) =
(√31)/(√3–1) = ab√2 In this sum it should be ab√3, not ab√2 (√31)/(√3–1)=ab√3 => (√31)(√31)/(√3–1)(√31)=ab√3 => (√31)^2 What is the coordinate points of (1/2,√3/2) when reflected to quadrant 3?Cot(21) = Write cot(21) in terms of tan Since 21° is less than 90, we can express this in terms of a cofunction cot(θ) = tan(90 θ)




How Sin 60 Is Equal To 3 2 Quora



How To Simplify Math Frac 3 Sqrt8 Frac 1 Sqrt2 Math Quora
Let a tangent be drawn to the ellipse x^2/27 y^2 at (3√3 cos θ, sin θ) where θ ∈ (0, π/2 ) Trigonometry ML Aggarwal ISC Class11 Maths Understanding Solutions Chapter3 Step by step Solutions of ML Aggarwal ISC Class11 Mathematics with Exe11, Exe12, Exe13, Exe14, Exe15, Exe16, Exe17, Exe18, Exe19, Exe110 and Chapter Test Questions Visit official Website CISCE for detail information about ISC Board Class11TO PROVE 1/(2√3) is irrational We can rationalize the denominator of the above expression, & then we can proceed with our proof After rationalization 1 / (2√3) * (2√3) / (2√3) = (2




Square Root Of 2 Wikipedia




How To Solve 1 1 2 2 3 Quora
If x tan 45° cos 60° = sin 60° cot 60°, then x is equal to A 1 B √3 C 1/2 D 1/√2 asked May 18 in Trigonometry by Yaana ( 354k points) trigonometryUse the Unit Circle to evaluate the trigonometric functions where sin θ = y and cos θ = x sin 0 = 0 sin π 6 = 1 2 sin π 4 = √ 2 2 sin π 3 = √ 3 2 sin π 2 = 1 cos 0 = 1 cos π 6 = √ 3 2 cos π 4 = √ 2 2 cos π 3 = 1 2 cos π 2 = 0 So if you recall, the short leg is 1/2 the hypotenuse, so the ycoordinate is 1/2, and the long leg is √3 times the shorter leg, or (√3)/2, so the xcoordinate is (√3)/2 The coordinates of that point are ((√3)/2,1/2) Now use the identities in the previous step to find that




4 The Square Root Of 3 Sqrt 5 Is A Sqrt 3 2 1 Sq
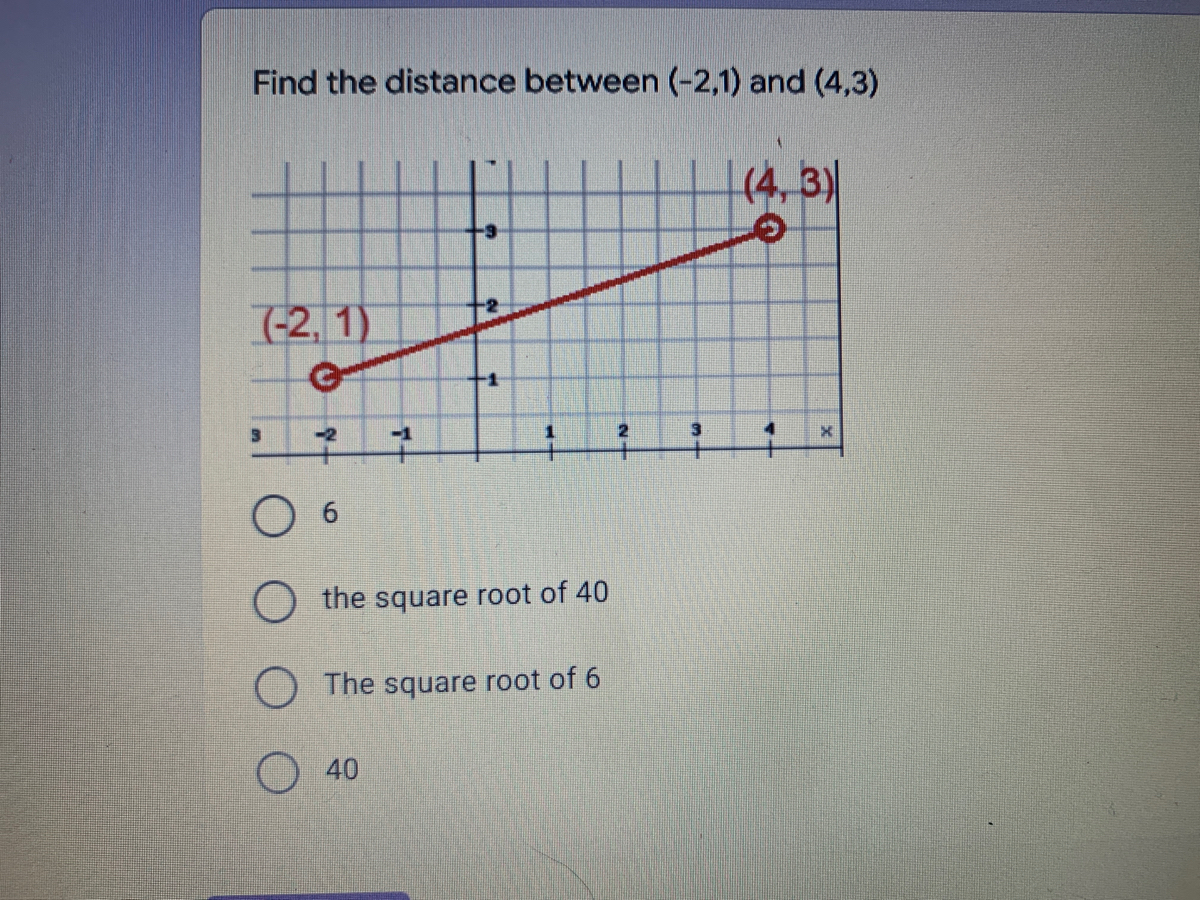



Answered Find The Distance Between 2 1 And Bartleby
The value of √3−2√2 is B √3/2 C √2/2 D 1/2 Answers 1 Get ↓ Other questions on the subject Mathematics Mathematics, 10, sara66 Which of the following correctly justifies statement four of the two column proof?Start studying Unit Circlefill in the blank Learn vocabulary, terms, and more with flashcards, games, and other study tools



If X 3 2 2 Then What Is The Value Of X 1 X Quora




Solving Quadratic Equations By Square Root Method By
OH = 1 cmThen DO = 2 * 1 = 2 cm, and DH = DO HO = 2 1 = 3 cm We define the side of the triangle ВСD through the height DH DН = ВС * √3 / 2 ВС = 2 * DH / √3 = 2 * 3 / √3 = 6 / √3 = 2 * √3 cm Determine the area of the base of the pyramid Sbn =In triangle ABC, A B C = 180° => (AB)/2 = 90° C/2 => Sin (AB)/2 = Sin (90°C/2) => √3/2 = Cos C/2 => C/2 = 30° => Sin C/2 = sin 30° => Sin C/2 =1/2If the terminal side of an angle θ in standard position intersects the trigonometric circumference at the point P (−1 / 2, √3 / 2) then the value of cotθ is;




Extract The Square Root Of A 2 Left Frac Left 3a Sqrt A Right 2 Right Left Frac Left 3 Sqrt A Right 2 Right Frac 41a 16 1 Mathematics Stack Exchange




If X 2 Root 3 Find The Value Of X 1 X Whole Cube Brainly In
If tan θ=√32 the sum of the infinite series 1 2 1−cos If t a n θ = √ 3 2 , the sum of the infinite series 1 2 ( 1 − c o s θ ) 3 ( 1 − c o s θ ) 2 4 ( 1 − c o s θ ) 3 ∞ isThe necessary and sufficient condition for the line TO REPRESENT a (30°,60°,90°) triangle is THIS 1) The longest side is twice the shortest side, and 2) The square of the longestTherefore we end up with (1/2, √3/2) and can conclude that sin(1°) or sin(2π/3) is equal to 1/2 and cos(1°) or cos(2π/3) is equal to √3/2 Finding Sine and Cosine Third Quadrant This is exactly the same as Finding Sine and Cosine Second Quadrant , except for step five, we now negate both value of the ordered pair
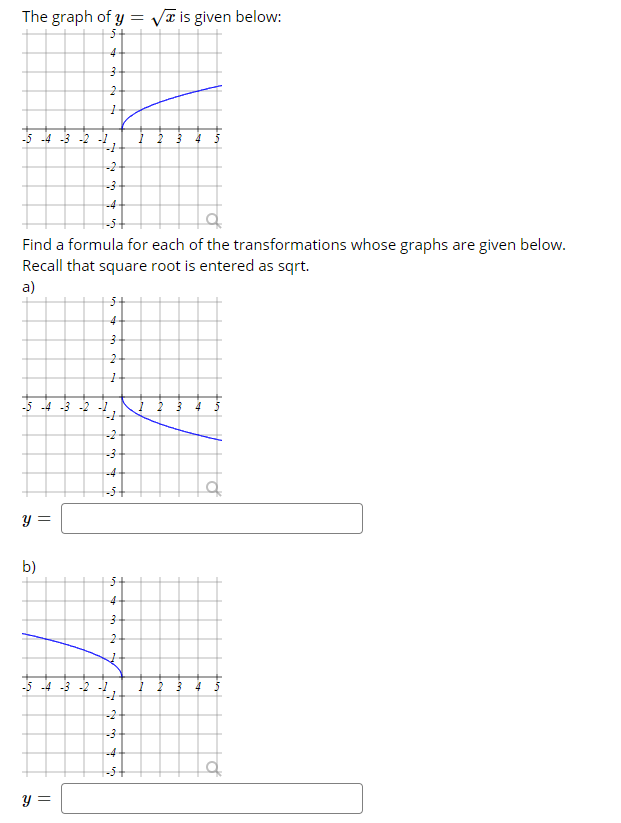



Answered The Graph Of Y Vt Is Given Below 4 Bartleby
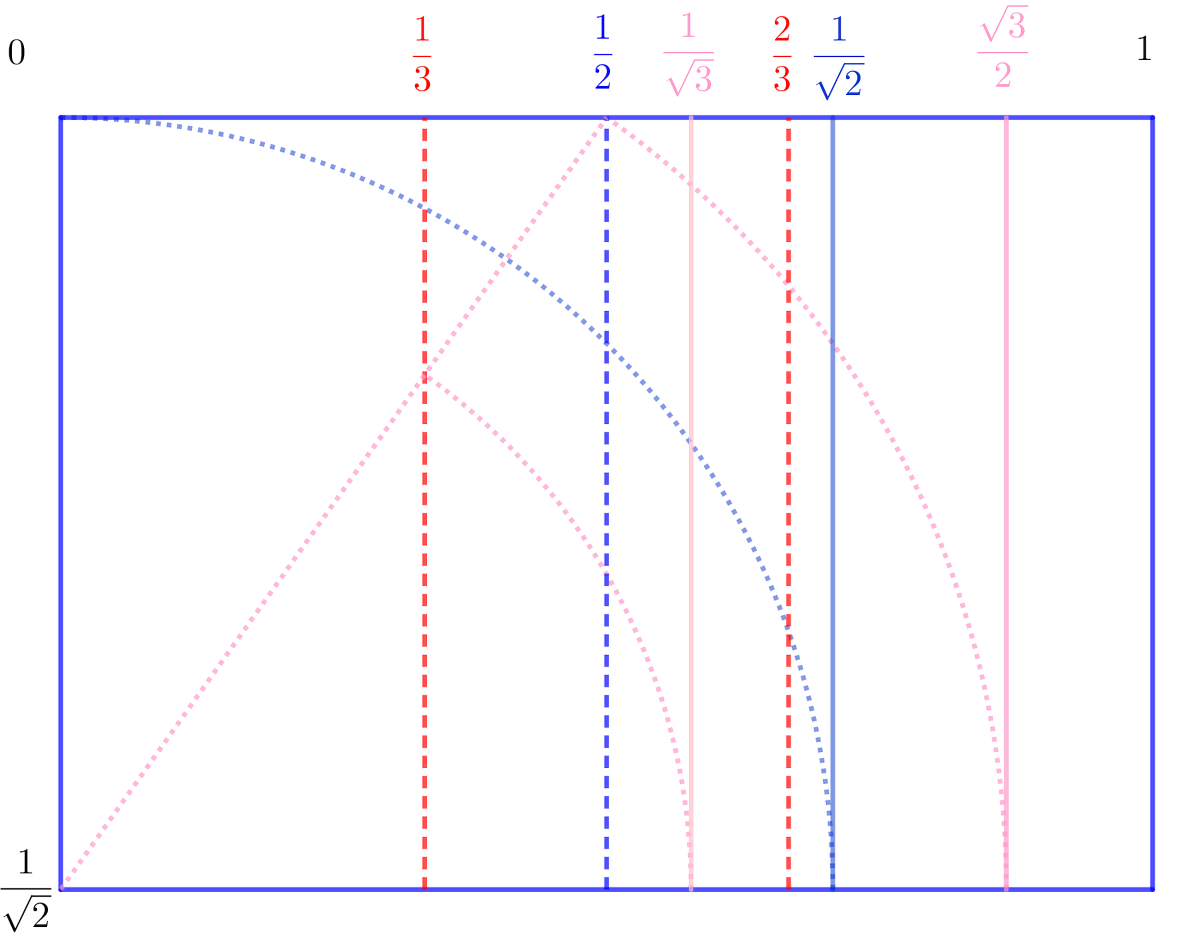



Christian Mercat And What Is A The Root Of Thirdsday Well The Inverse Of The Square Root Of 3 Day Which Is Easily Drawn On An Paper Reminding
4 Let P = a i j be a 3 × 3 matrix and let Q = b i j where b i j = 2 i j a i j for 1 ≤ i, j ≤ If the determinant of P is 2, then the determinant of the matrix Q is 5 If the sum of n terms of an AP is given by S n = n 2 n, then the common difference of the AP is 6 Therefore we end up with (1/2, √3/2) and can conclude that sin(1°) or sin(2π/3) is equal to 1/2 and cos(1°) or cos(2π/3) is equal to √3/2 Finding Sine and Cosine Third Quadrant This is exactly the same as Finding Sine and Cosine Second Quadrant , except for step five, we now negate both value of the ordered pair0 9 2 1 2 4 C = Tchol(A) = √ DL = 0 3 Problem 65, #26 TIn the Cholesky factorization A = CTC, with C = L √ D, the square roots of the pivots are on the diagonal of C Find C (upper triangular) for ⎡ ⎤ ⎡ ⎤ 9 0 0 1 1 1 A = ⎣ 0 1 2 ⎦ and A = ⎣ 1 2 2 ⎦ 0 2 8 1 2 7 Solution (4 points) For the first matrix A, we have




Integral 2x 3 2 1 4x 4 6 Dx Integral Chegg Com




Solve Solve Inequalities With Step By Step Math Problem Solver
= 1 / 2√3 = (1 / 2√3) x (2√3 / 2√3) So, cot 15 0 = 2 √3 So, on putting the values of cot 15 0 and tan 15 0 in equation (i), we will get = (2 √3) 2 (2 √3) 2 = 4 3 2√3 4 3 2√3 = 14 Let's see how we can learn it 1In sin, we have sin cos In cos, we have cos cos, sin sin In tan, we have sum above, and product below 2For sin (x y), we have sign on right For sin (x – y), we have – sign on right right For cos, it becomes opposite For cos (x y), weClick here👆to get an answer to your question ️ Evaluate sin^1 {cos (sin^1 √(3)2) } Join / Login maths Evaluate sin − 1 {cos (sin − 1 2 3 )} Answer Given, sin − 1 {cos (sin − 1 2 3 )} = sin − 1 {cos (6 π )} = sin − 1 (2 3




Square Root Of 3 Wikipedia




Ex 2 1 14 Find Value Of Tan 1 Root 3 Sec 1 2 Ex 2 1
All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction \frac {1} {2}x^ {2}x3=0 2 1 x 2 x − 3 = 0 ThisA corresponding angles theorem b transitive property of equality c vertical angle theorem d substitution property of equalityRelated Questions Which of hte following figures lie on hte same base an;




Sin 30 1 2 And Cos 30 Square Root 3 3 True Or False Help Me Brainly Com




1 1 2 1 2 3 1 3 4 1 4 5 1 5 6 1 6 7 1 7 8 1 8 9 2 Mathematics Topperlearning Com Lbve3ydd
C is the circle with equation x^2 y^2 = 1 Q(1/2, √3/2) is the point on C The equation of the tangent to C at the point Q can be written in the form y = axb Find the value of a and find the value of bClick here👆to get an answer to your question ️ Simplify 1/1 √(2) 1/√(2)√(3) 2/√(3)√(5) A rightangled triangle with angles of 60° and 30° has sides in the ratio 1√32 The core angle of √3 2 is 60° However, the negative sign indicates that we are working with an angle in the 3rd or 4th quadrants In the 3rd quadrant θ = 180° 60° = 240° In the 4th quadrant θ = 360° − 60° = 300° sin−1( √3 2) = 240° or



Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 Studyrankersonline
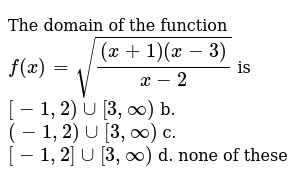



The Domain Of The Function F X Sqrt X 1 X 3 X 2 Is 1 2 Uu 3 Oo B 1 2 Uu 3 Oo C 1 2 Uu 3 Oo D None Of These
The final transformation Matrix contains 4 elements and those are T00=1/2 T01=√3/2 T10=√3/2 T11=1/2 And the matrix is T=1/2 √3/2;√3/2 1/2 If you have any questions regarding this answer let me know in comments section below Image transcriptionsDegrees Radians Sin Cosine Tangent Cotangent Secant Cosecant 0 0 0 1 0 undefined 1 undefined 30 π/6 1/2 √3/2 √3/3 √3 2√3/3 2 45 π/4If y(x) is solution of DE √(1x^2 ) dy/dx√(1y^2 )=0, Such that y(1/2)=√3/2 then(a) y(1/√2)=1/√2(b) y(1/√2)=√3/2(c) y(1/√2)=1/√2(d) y(1/2)=1/2To



Solve Equations With Square Roots Elementary Algebra
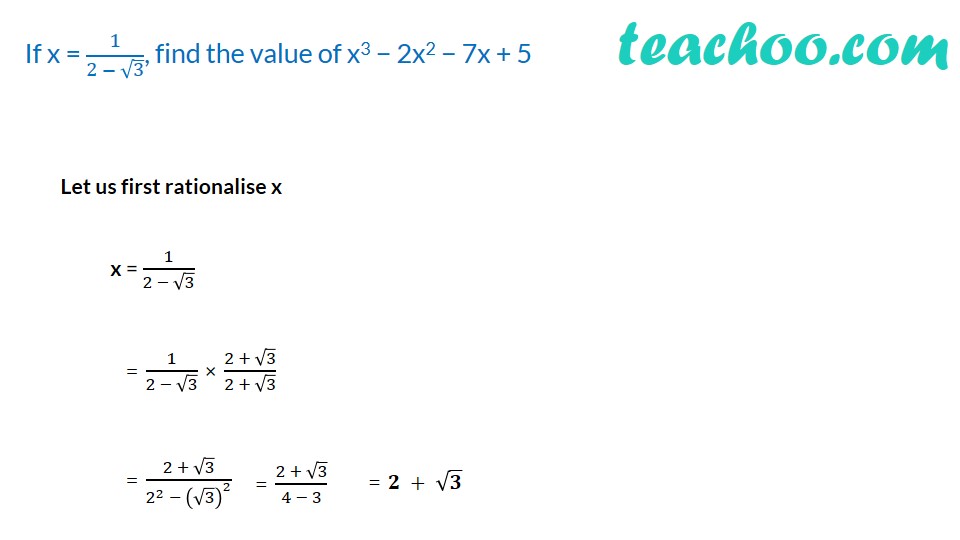



If X 1 2 3 Find The Value Of X 3 2x 2 7x 5 Video T
The difference of squares identity can be written − B2 = (A− B)(A B) This is the key to eliminating square roots from the denominator Note that (1 − √2 √3) is only a partial conjugate for (1 √2 √3) Multiplying these two expressions will eliminate terms in √2 but leave terms in √3 If we want to rationalise the Another way to think about it is that the base is √3/2 times the length of the hypotenuse and the height is 1/2 times the length of the hypotenuse So, if instead, the hypotenuse is a length of 7, our triangle base will be 7 x √3/2 = 7√3/2 The triangle height will have a length of 7 x 1/2A 1/2, √3/2, 1 B √2, √6, 2 √2 C 5/2, 5 √3/2, 10 D 3, 3 √3, 6 Answer by ikleyn() (Show Source) You can put this solution on YOUR website!



A Point On A Terminal Side 1 2 Sqrt 3 2 Youtube




Ex 2 1 7 Find Principal Value Of Sec 1 2 Root 3 Chapter 2
This is a triangle whose three angles are in the ratio 1 2 3 and respectively measure 30° (π / 6), 60° (π / 3), and 90° (π / 2)The sides are in the ratio 1 √ 3 2 The proof of this fact is clear using trigonometryThe geometric proof is Draw an equilateral triangle ABC with side length 2 and with point D as the midpoint of segment BC√(3 2√2) Math Tricks That Will Blow Your MindMathematics is the only thing that can analyze everything in the world This episode is designed in such a wSin 30° = 1/2 cos 30° = √3/2 sin 60° = 3/2 cos 60°= 1/2 Now, substitute the values in the given problem sin 60° cos 30° sin 30° cos 60° = √3/2 ×√3/2 (1/2) ×(1/2 ) = 3/41/4 = 4/4 = (ii) 2 tan 2 45° cos 2 30° – sin 2 60 We know that, the values of the trigonometric ratios are sin 60° = √3/2 cos 30° = √3/2




Square Root Of 229 How To Find Square Root Of 229 Solved




Simplify 1 1 2 1 2 3 1 3 4 Brainly In
For each of them, you want to multiply the numerator and denominator by the conjugate of the denominator 1/(2 √3) * (2 √3)/(2 √3) = (2 √3)/(2^2 Transcript Example If A = 8(3&√3&2@4&2&0) and B = 8(2&−1&2@1&2&4) Verify that (i) (A')' = A, A = 8(3&√3&2@4&2&0) A' = 8(3&√3&2@4&2&0(sin4𝜋/3)=−√3/2 tan(5𝜋 3)= sin(5𝜋 3) cos(5𝜋 3) =−√3/2 1/2 =−√3 csc(7𝜋 6)= 1 sin(7𝜋 6) = 1 −1/2 =−2 −cos1(1/2)=𝜋 3 −sin1(1)=𝜋 2 Important Identities Unit Circle Identity )sin2(𝜃cos2(𝜃)=1, and dividing this by cos2(𝜃)gives tan2(𝜃)1=sec2(𝜃) HalfAngle Identities (cos2( )=1 2 1cos(2



1
/calculate-a-sample-standard-deviation-3126345-v4-CS-01-5b76f58f46e0fb0050bb4ab2.png)



How To Calculate A Sample Standard Deviation




Chapter 7 Radicals Radical Functions And Rational Exponents Ppt Video Online Download




A Cambridge Interview Problem Sqrt 3 2sqrt 2 Youtube




Rationalize The Denominator Of 1 3 2 Under Root 2 Under Root 5 Mathematics Topperlearning Com 8pvu0x66




Free Math Answers Answers Within 24 Hours Step By Step Explanations




30 60 90 Triangle Explanation Examples



If X 1 Root2 Root3 Prove That X 4 4x 3 4x 2 16x 8 0 Cbseassistance
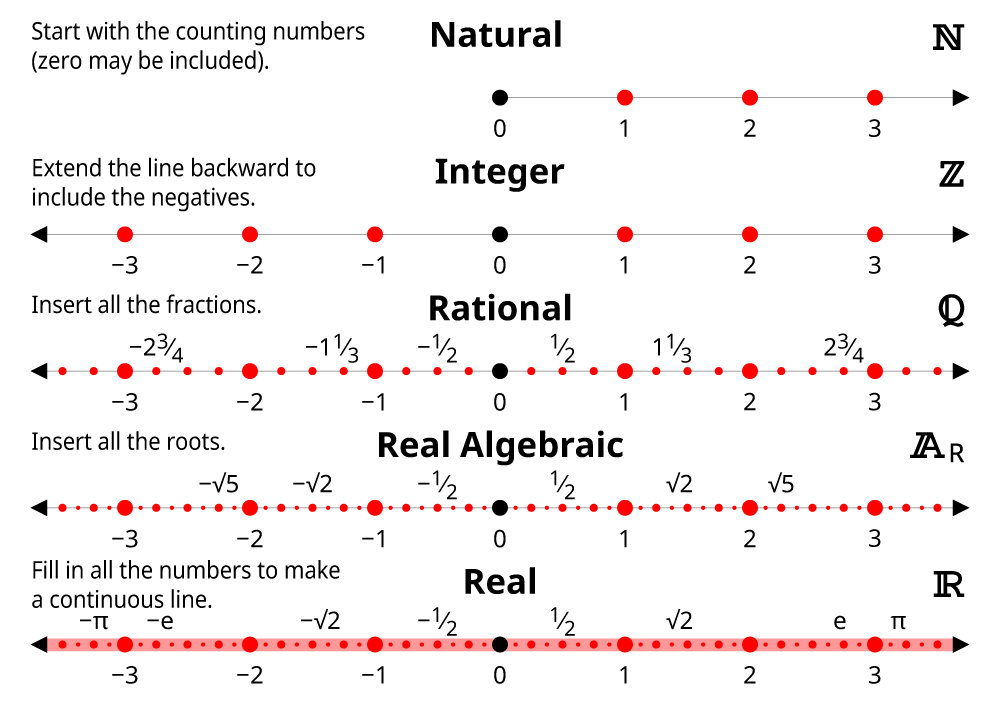



Number Sets




A 3 2 2 Then The Value Of A 1 2 A 1 2 Can Foundation Brainly In




Special Right Triangles Review Article Khan Academy




Multiplying And Dividing Radical Expressions



How Do You Find The Exact Value Of Arccos 1 Sqrt 2 Socratic



If X 3 2 2 Then What Is The Value Of X 1 X Quora




Strategy And Trick To Find Square Root Of 8 2 15 Radical Expressions Youtube




1 Sqrt 2 Sqrt 3 Sqrt 5 1 Sqrt 2 Sqrt 3 Sqrt 5 In




Square Root Of 3 Wikipedia
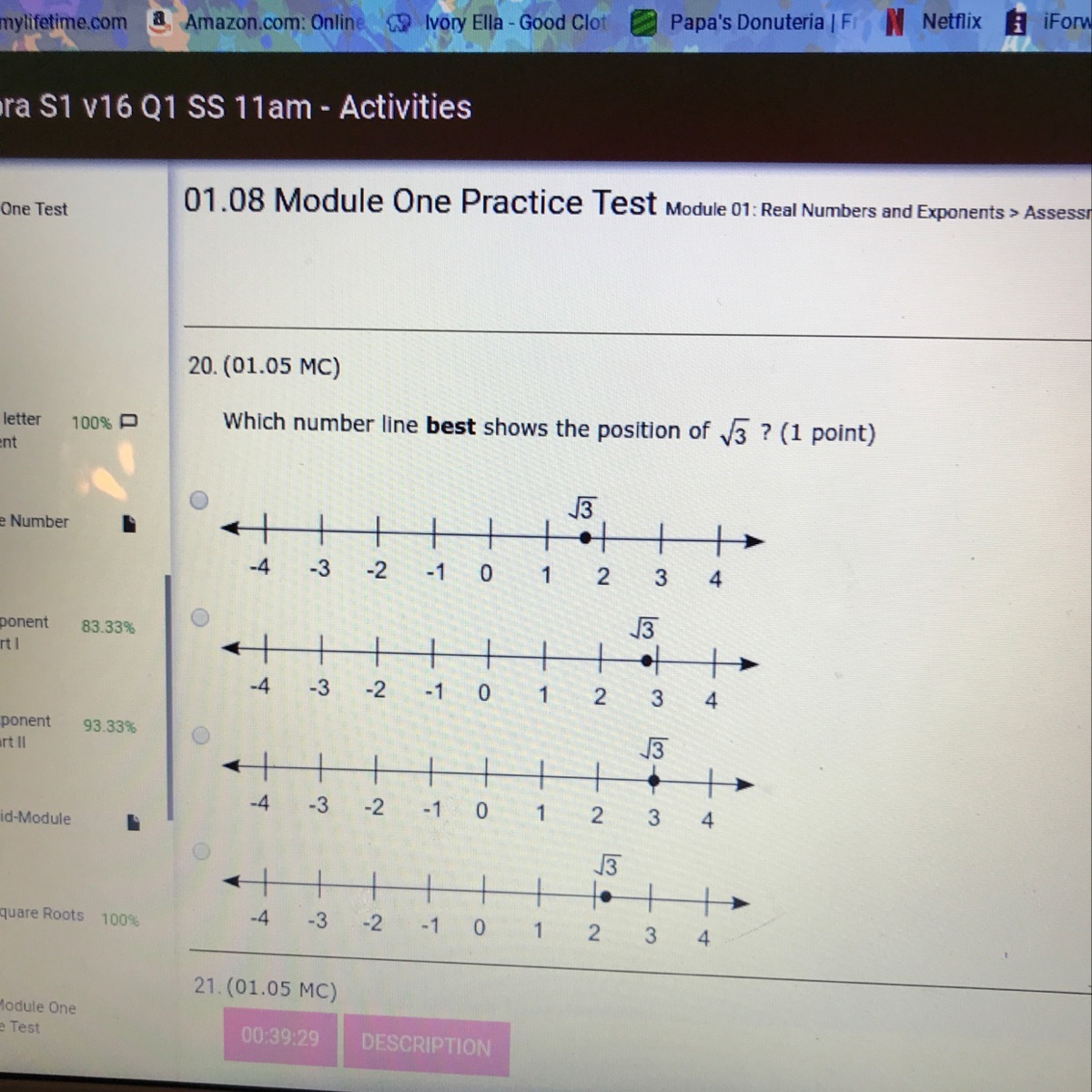



What Number Line Best Shows The Position Of Square Root 3
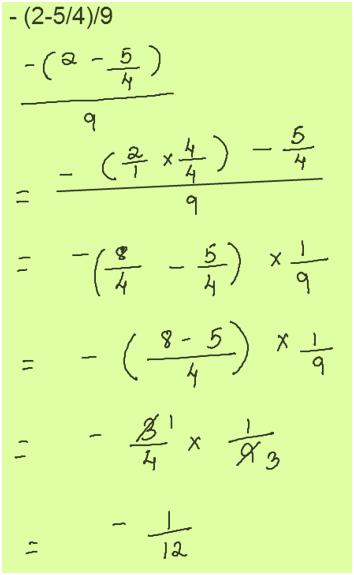



Free Math Answers Answers Within 24 Hours Step By Step Explanations




How To Find 1 2 Of 2 3 Video Lesson Transcript Study Com




Solving Radical Equations




For A Complex Number 1 2 J Square Root 3 2 Find Chegg Com
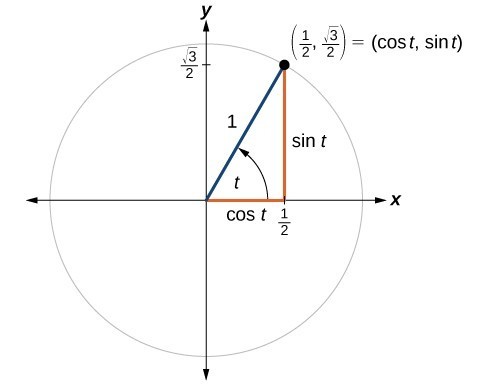



Unit Circle Sine And Cosine Functions Precalculus Ii




Example 18 Rationalize The Denominator Of 1 2 Root 3




Is There A Solution For X For X 2 Y Sqrt 3 X 2 2 1 Mathematics Stack Exchange




If X 3 2 2 Then Check Whether X 1 X Is Rational Or Irrational Cbse Class 9 Maths Learn Cbse Forum
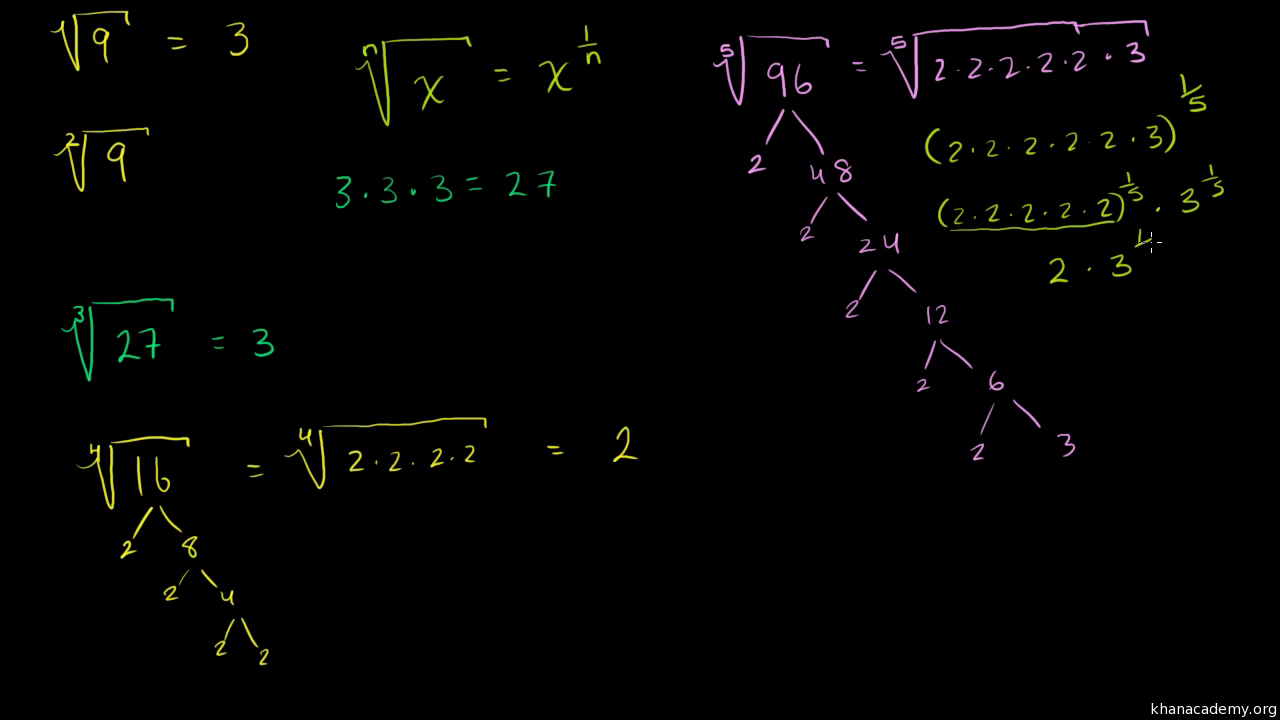



Simplifying Higher Index Roots Algebra Video Khan Academy




Rationalize 1 7 3 2 Maths Questions




How To Do This Question X 3 1 2 Find Value Of 4x 3 2x 2 8x 7 Mathematics Topperlearning Com 4r5prjll



View Question Sqrt 3 2 Divide By 1 2
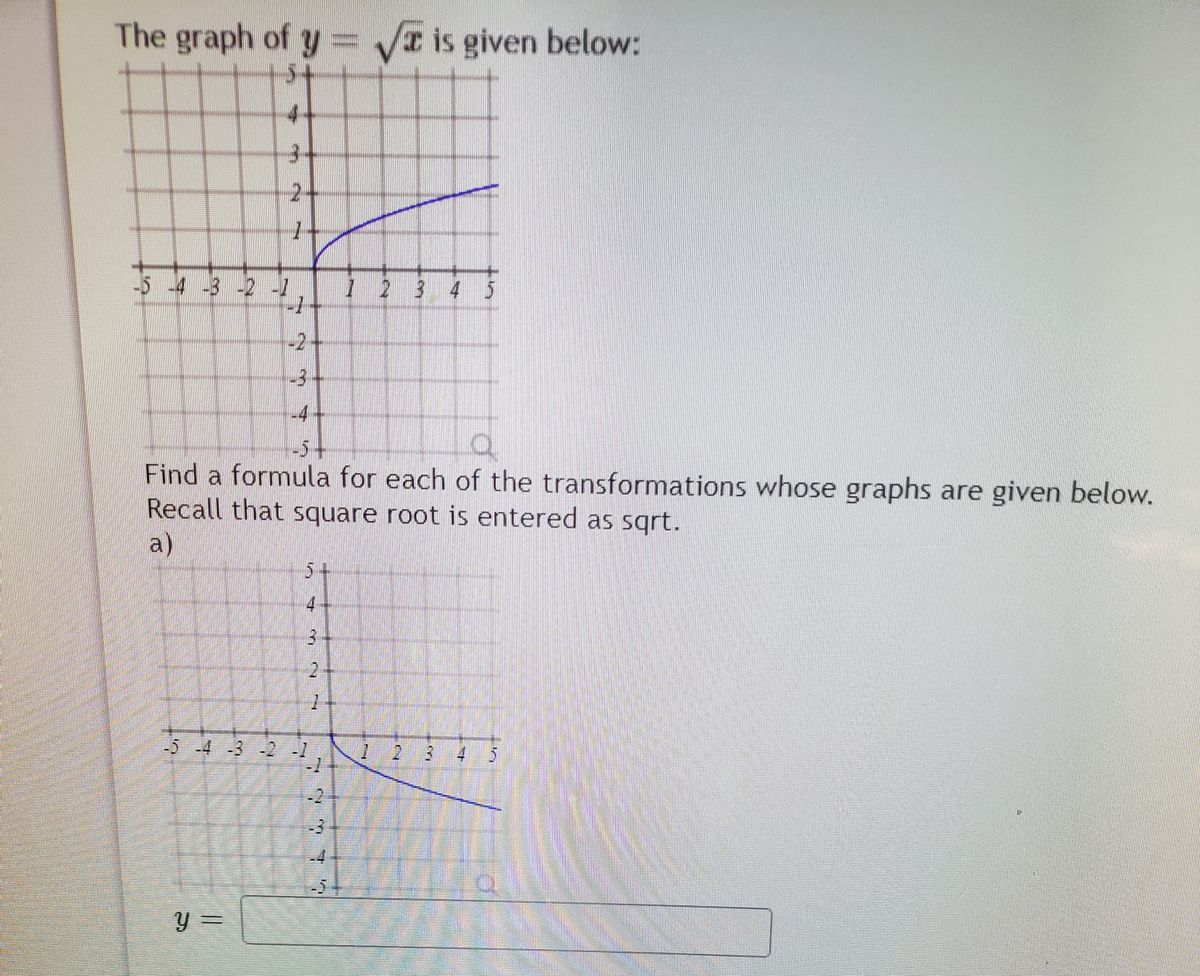



Answered 5 4 3 2 1 4 2 3 4 5 Find A Bartleby




Simplify 8 2 3 9 10 0 1 144 1 2 Brainly In




Square Root Of Frac216 2 3 25 1 2 1 25 3 2 Gauthmath
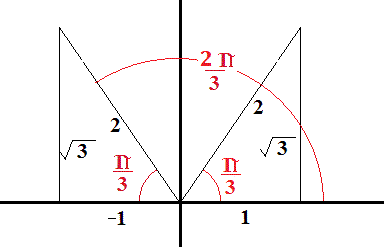



What Is The Sin 1 Sqrt 3 2 Socratic




If N Square Root 3 2 2 Square Root 3 2 2 Square Root 3 1 2 Square Root 3 1 Then N Equal To 1 Maths Number Systems Meritnation Com




0 01 2 Square Root Of 5 6 1 3 1 2 1 3 Gauthmath
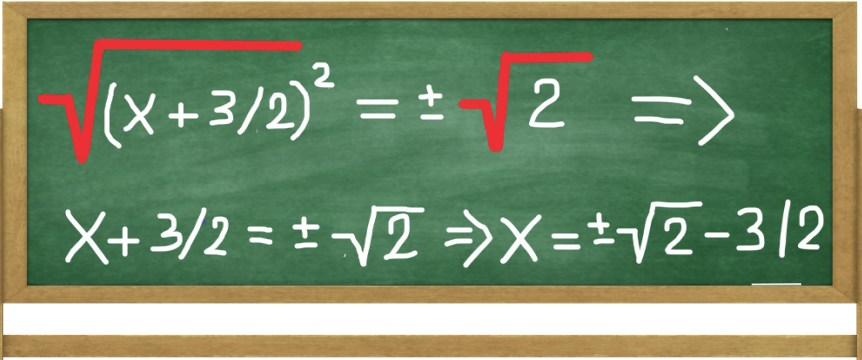



Completing The Square Formula How To Complete The Square With A Quadratic Equation




Types Of Numbers Difference And Classification
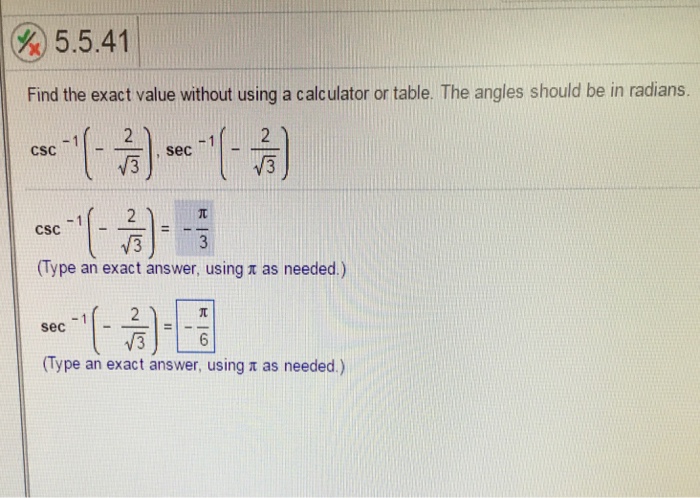



What Is The Answer To Sec 1 2 Square Chegg Com




Find The Sum 1 1 Sqrt 2 1 Sqrt 2 Sqrt 3 1 Sqrt 3 Sqrt 4 Youtube




Eq 11 The Higher Curve And The Square Root Of Eq 10 The Lower Download Scientific Diagram




Square Root Of 2 Wikipedia




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter Geometric Progressions Download Free Pdf Available
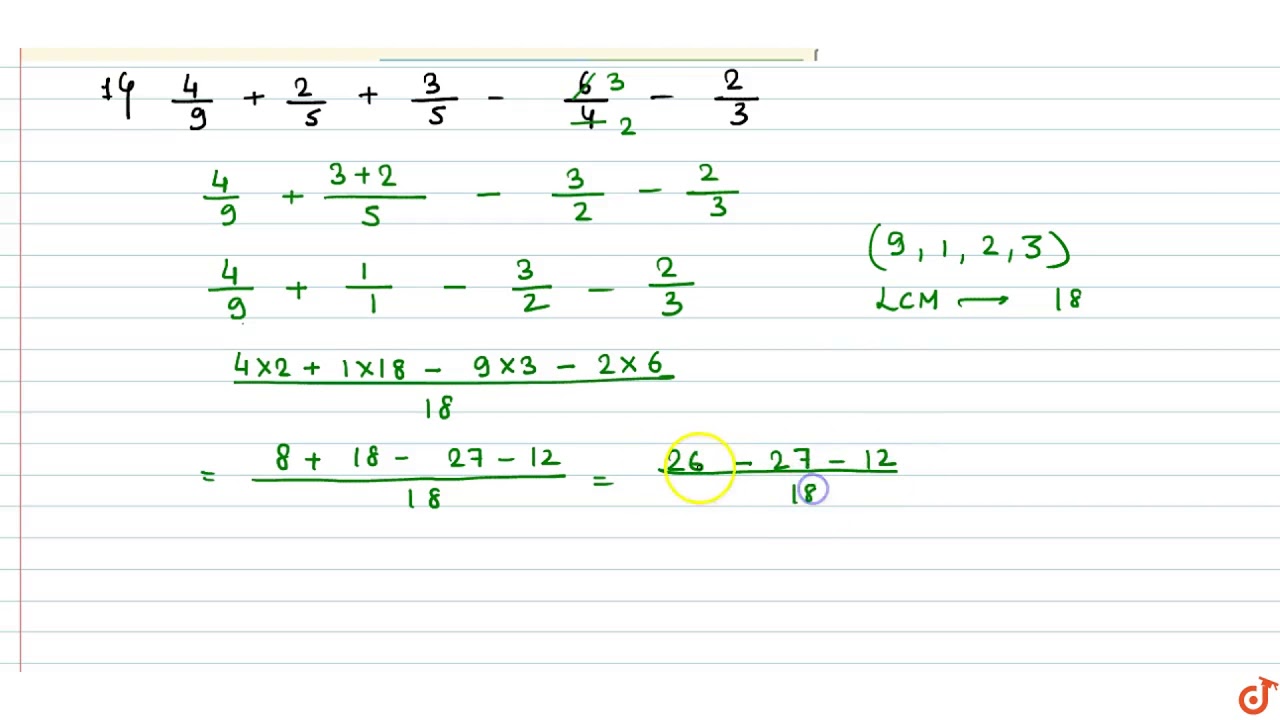



Simplify The Expressions 1 4 9 2 5 3 5 6 4 2 3 2 11 2 8 3 4 2 5 Youtube



If X 3 2 2 Then What Is The Value Of X 1 X Quora




Solved If X 3 2 2 Check Whether X 1x Is Rational Or Irrational Self Study 365



Q Tbn And9gcsb2rnpibjsemfefshm1leviszzhattq67fri0obpzhq J Lxfh Usqp Cau
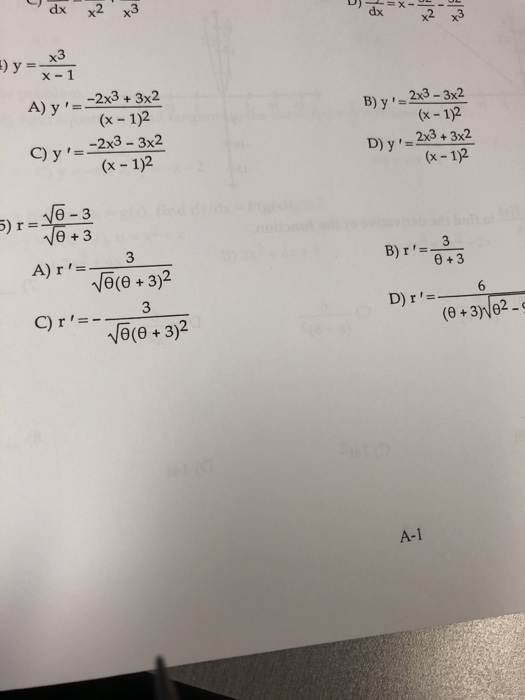



R Square Root Of Theta Minus Three Divided By The Chegg Com




Review Topics Ch R 1 In College Algebra




Rationalize The Denominator Squareroot 1 2 Chegg Com



If X 3 2 2 How Do You Show That X 1 X 2 Quora




Simplifying A Square Root Expression By Writing It As A Square Learnmath




2 3 2 3 2 3 2 3 3 1 3 1 Simplify Brainly In




2 3 2 1 3 3 10 4 1 Square Root Of 1 2 Gauthmath



Bisection Method
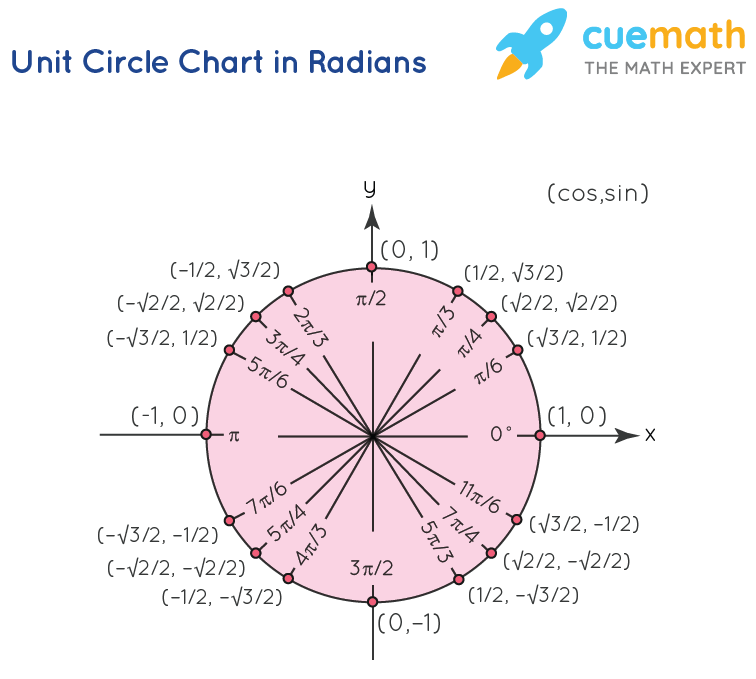



Unit Circle Equation Of A Unit Circle Unit Circle Chart




Solved Find Rational Numbers A And B Such That I 2 1 2 1 A B Self Study 365




Simplify 2 5 3 1 3 2 3 5 2




The Domain Of The Function F X Sqrt X 1 X 3 X 2 Is 1 2 Uu 3 Oo B 1 2 Uu 3 Oo C 1 2 Uu 3 Oo D None Of These




Simplifying Radical Expressions




Wolfram Alpha Examples Step By Step Solutions




Simplify 1 2 3 2 5 3 1 2 5 Brainly In



Q Tbn And9gcqt8xcypqw0rmdh64vbuopwz1cxhnbqpt756epqa I9o2cblok Usqp Cau



What Is The Value Of 3 2 2 Quora




Square Root 2 3 Cannot Be Equal 1 3 1 2 2 6 2 2 3 2 3 1 4 3 1 2 Maths Number Systems Meritnation Com



Frac Square Root Of 1 3 4 Cube Root Of 2 3 1 Gauthmath




How Do You Evaluate Cos 1 Sqrt3 2 Socratic



1



Square Root Calculator Find The Square Root In One Easy Step



What Is The Principal Value Of Cos 1 3 2 Sarthaks Econnect Largest Online Education Community
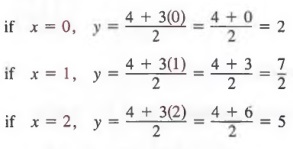



Graph Graph Equations With Step By Step Math Problem Solver
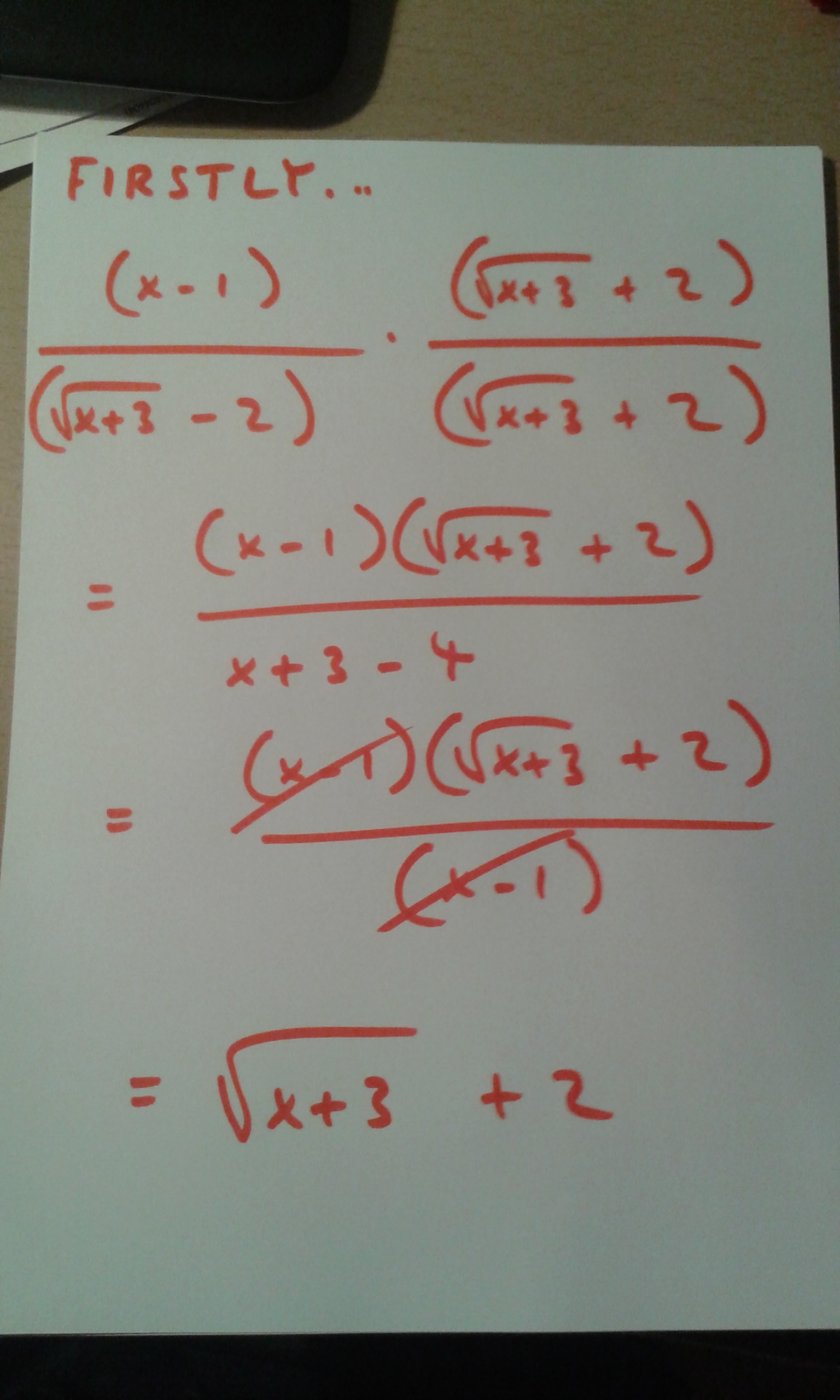



How Do You Find The Limit Of X 1 Sqrt X 3 2 As X Approaches 1 Socratic



View Question Square Root 3 2 1 2 210 Degrees 7pie 6 Find Sin Cos Tan Cot Csc And Sec




Rationalise The Denominator Of 1 2 Sqrt 3 Youtube




Simplifying Radical Expressions




Square Root Of 2 Wikipedia



Simplify 3 Root 3 2 Root 2 Youtube



Express Each One Of The Following With Rational Denominator I 1 3 2 Ii 1 6 5 Iii 16 41 5 Sarthaks Econnect Largest Online Education Community



0 件のコメント:
コメントを投稿